The initialization of weights in a neural network is a crucial step in the training of the network. The proper initialization of weights can help the network to learn faster and avoid local minima. There are a few different methods for weight initialization, such as random initialization and Xavier initialization.
It is a design parameter that is sensitive to the failure of the wrong choice because it may slow down or stall the convergence. It would be easy to guess that the first number would be zero, but it also resulted in 0 gradient, implying that no learning occurred. Another option is to randomly sample points from the distribution. The distribution’s spread is determined by these values. In this blog post, I explain how neural networks work and show you how to use them. In this paper, a deep residual learning training for image recognition was used. He Initialization was used to train ResNets.
When Batch Normalization was released in 2015, the significance of weight initialization was less pronounced. The study demonstrates that weight initialization is still a necessary field of research. If you want to see other projects, check out my GitHub and Medium profiles.
In Step 1, the Neural Network is introduced, beginning with the allocation of weights and biases. For every layer, we compute a linear combination of inputs and weights (Z) and then apply activation function to the linear combination (A) with inputs and weights (X, W, and biases b) input input.
All derivatives in a given W will remain the same regardless of whether the weights are initialized to zeros or not. As a result, neural cells will be able to distinguish between the multiple iterations. Failure to break symmetry is the name of this issue. There is no such thing as a zero result, even if there are constant initialization.
When all weights are initialized to 1 and each unit receives signal equal to the sum of inputs (and outputs sigmoid(sum(inputs)), that is, when all weights are initialized to 1. If all weight units are zeros, it is even worse; each hidden unit will be out of sync. All units within the hidden layer will be the same regardless of what was input, no matter what was given.
How Weights Are Initialized In A Network?
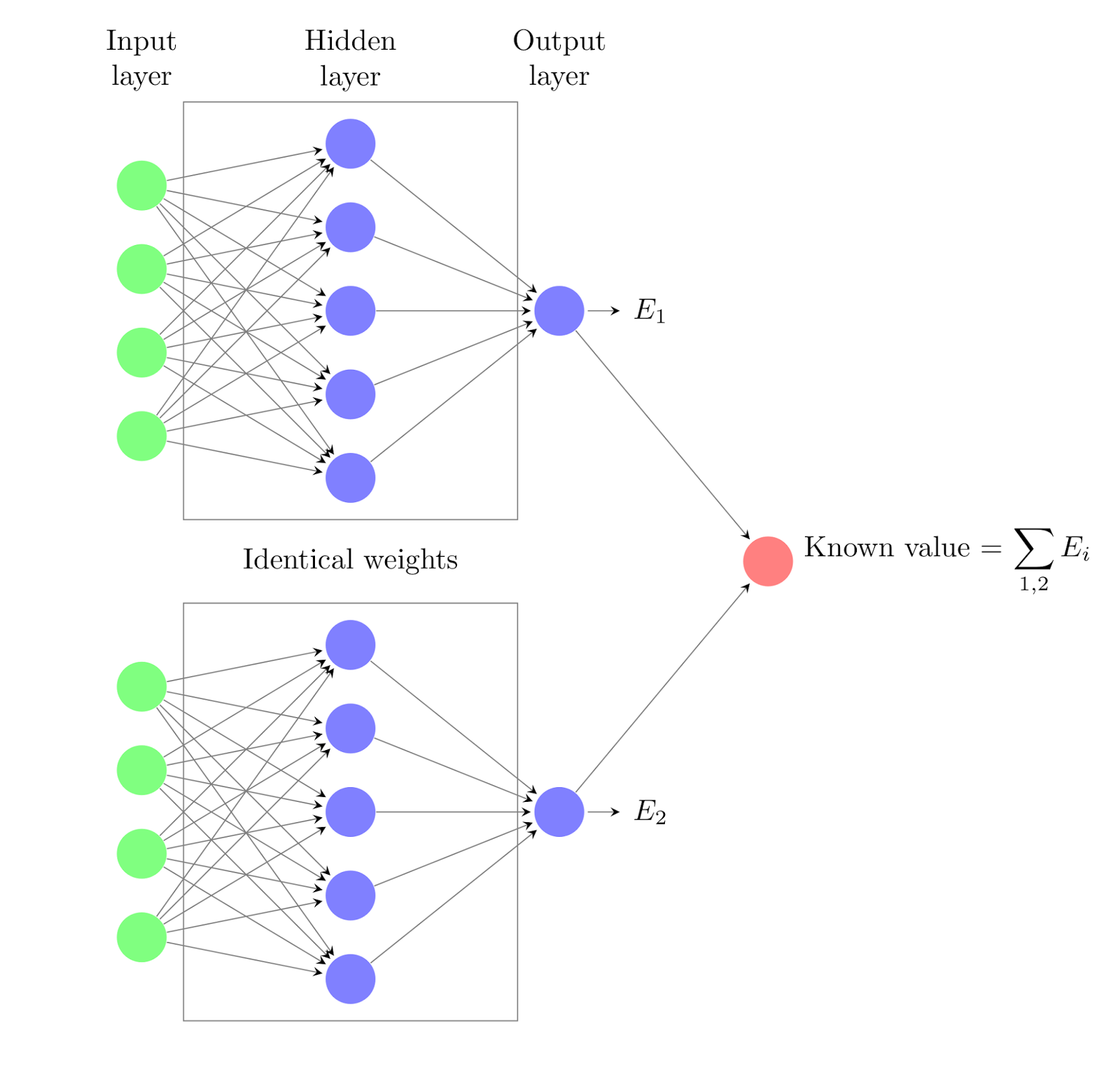
It entails setting the weights of a neural network to small random values that define the starting point for algorithm implementation (learning or training).
In this step-by-step method, we will go over the reasons why a strong weight initialization is required for deep neural nets. Several approaches have been proposed in the last few decades, and we will go over which works best in the contemporary network architecture. If the weight is too large, the network will fail to learn. When initialized too small, weights may appear to be too small. Where do you find the sweet spot? We can simulate forward passes by using neural networks. This pass completely eliminates each layer’s activation.
In the following example, we saw that our layer outputs exploded after 29 consecutive matrix multiplications. In our network architecture, for example, we want the output of each layer to be around a one-standard deviation. This theoretically could allow us to repeat matrix multiplications across as many layers as we want without activations exploding or vanishing. Understanding the difficulty of training deep feedforward neural networks was a seminal paper authored by Xavier GLOrot and Yoshua Bengio in 2010. Using standard weight initialization on a 100-layer tanh network results in activation gradient variations that are roughly the same size as they were before, albeit infinitely small. The standard deviation of the activation outputs of the 100th layer is currently around 0.08, but activations have not completely vanished. We’d like the activation outputs of layers to have a mean of 0 and a standard deviation of 1 with ReLU activation functions like tanh and softsign.
If we scale the weights from this number to their values, we will see that each ReLU layer deviates by one on average. et. have no affiliation with either the They have proposed a new initialization scheme for deep neural nets using asymmetric, non-linear activations. When using Xavier to.initialize weights, activation outputs nearly disappear by the 100th layer. They also trained even deeper networks using ReLUs, as He and his team did. The 30-layer CNN was discovered to use Xavier. It stalled completely and was unable to learn anything at all. When the same network wasinitiated according to the three-step procedure outlined above, it had a significant increase in convergence.
It ensures that the neural network can learn from its mistakes and improve its performance over time. Because the network will not be biased in its decision making with random weights, making predictions based on random weights is critical. Machine learning and artificial intelligence tasks frequently use this technique because it is simple to learn and can find solutions to problems quickly. When a network’s weights are randomly initialized, it will be able to learn from data and improve performance over time.
Initializing Weights In A Neural Network
It is critical to assign weights to neural networks in order to optimize them for the task at hand. When weights are initialized to zeros, the derivatives are the same for every neuron in the network, implying that the network learns the same features over time. This may result in the network failing to break symmetry, as well as the issue of generalizations. As a result, if the neural networks are properly configured, it is possible to optimize them for the task at hand, allowing for more accurate and precise predictions.
How Do You Initialize Weights In Neural Network Pytorch?

Weights can be initialized in many ways in a neural network. The most common way is to initialize the weights randomly. This can be done by initializing the weights to small random values. Another way to initialize the weights is to initialize them to a constant value.
When learning how to initialize model weights, it is critical to comprehend them. A significant factor in determining the outcome of training is the initial weight. It’s unfortunate that an incorrectly initialization of weights can result in gradient explosions or vanishing. The user is expected to have a basic understanding of PyTorch in this article. A weight initialization method with non-linear activation, such as Xavier(Glorot) and Kaiming, is one of two standard methods. We can distinguish between the uniform distribution and the normal distribution of data by taking into account the samples. If you use the fan_in mode, the data will remain undamaged after an explosion or implosion.
If you put your back pedal in fan_out mode, gradient epochs will be preserved. It is worth noting that ReLU gains from time to time, whereas LeakyReLu loses. We usually gain something when the kaiming_uniform_(1/a*2 +1) is used, which specifies only the type of non-linearity we are dealing with. Layers are sampled into a normal distribution, with layer weights and input_dims representing dimensions and output levels, and the output and input dimensions are selected on the operating mode’s options.
How To Initialize A Laye
Before you initialize a layer, you must first compute a weight matrix. A weight matrix initialized with the same number of neurons as the number of neurons in the layer is commonly used. The weight matrix is then multiplied by the input matrix.
Why Is It Important To Initialize Weights In Neural Network?
There are a few reasons why initializing weights in a neural network is important. Firstly, if the weights are not initialized properly, the network may not be able to learn the desired function. Secondly, if the weights are not initialized properly, the network may be unable to converge to a solution. Thirdly, if the weights are not initialized properly, the network may be unable to generalize to new data. Finally, if the weights are not initialized properly, the network may be unable to optimize its performance.
The author assumes that the reader has basic understanding of neural network concepts, forward and backward propagation, activation functions, optimization algorithms, and so on. The first step in the implementation of a neural network is to consider the weight of the network in order to achieve the best and most optimal results. It is critical that you make proper weight initialization if you want to keep your learning process as simple as possible. Throughout the training program, the weights on the same neuron will remain constant. When the sigmoid activation function (logistic tanh) is used, the saturation problem can occur, which can lead to the vanishing gradient problem. All of these weighted sums will collapse in a21 due to the sheer number of neurons in the organism. How do I overcome this?
We can use random weights in a variety of distribution methods. The first contributors to this concept of better random weights initialization were Xavier GLOROT and He et al. Instead of using a standard normal distribution, use a normal distribution with k/n variance, which is defined in response to activation events. This method reduces the likelihood of the vanishing/explosing gradient problem because the weighted sum of inputs at a hidden layer does not take a large value.
Why Proper Weight Initialization Is Important
Our weights must be initialize for a variety of reasons. The first problem is that improper weight initialization can result in faulty activation outputs. Furthermore, it is possible that an improper weight initialization will result in a tedious and time-consuming learning process. We will look at the differences between weight initialization in the following sections, as well as how important they are. This type of initialization consists of a random number-one initialization. When we initialize our weights at random, we are trying to ensure that all neural layers are active at the same time. This is important because it ensures that network learning takes place in an unbiased manner. The second type is a derivation. These are the starting weights for the athlete. The gradual weight initialization method is one that is intended to gradually increase the amount of weight we are accustomed to. As a result, it will be necessary to gradually increase the weights depending on the performance of the network. This ensures that the network is gradually and consistently learning from data.
How To Initialize Weights In Neural Network Keras
There are a number of ways to initialize weights in a neural network using the Keras library. One way is to use the “glorot_uniform” function, which creates a uniform distribution of values between 0 and 1. Another way is to use the “lecun_uniform” function, which creates a uniform distribution of values between -1 and 1.
We’ve shown how to resolve the Re Initialize Weights Keras bug in practice by inspecting various real-world cases. The metrics, optimizers, and loss functions are all specified in compiled form. There is no correlation between modeling and weights because it allows you to construct a model as many times as you want without causing problems with pretrained weights. The compilation is the final step in the modeling process. It will perform updates to the weights you had previously specified. All units within a hidden layer will be the same if all weights in the hidden layer are the same. The main reason for initialize weights randomly is to address symmetry.
How To Initialize Weights And Biases In Neural Networks
Weights and biases can be initialized in a number of ways, but a common method is to use random values. This can be done by sampling from a uniform or normal distribution. Another method is to use Xavier initialization, which is designed to keep the scale of the gradients similar.
A neural network is made up of three layers and four nodes hidden beneath each layer. Many people prefer to use small constant values such as 0.01 to ensure that all ReLU units begin with the same trajectory and generate and propagate gradient. We will look at the impact of changing the bias in detail from 0 to anything else in this post. I looked into the impact of bias initialization on the loss of cross-entropy in a neural network. Two peaks are visible in the scatter plot, with one at 0.26 and the other at 0.33. There was no way to differentiate the data set from the rest. Despite this, I used this data set as an input to generate a separate decision boundary for a new NN.
How To Assign Weights In Neural Network
There is no one-size-fits-all answer to this question, as the appropriate way to assign weights in a neural network depends on the specific data set and task at hand. However, some general tips on how to assign weights in a neural network include: – Start by assigning random weights to the network nodes and connections. – Use a learning algorithm to adjust the weights based on the training data. – Try different weight initialization schemes and see what works best for your data set and task.
How does bias work in neural networks? During the absence of a thing, we are unable to comprehend its significance. If there are no weights involved, the slope of the line used to classify a data point remains constant, and we are unable to create a scalable line that separates two classes. If we look at b’s value of 0 and x1’s value of -x, we see the line equation (x2 = -x). As illustrated in the above plot, this figure is represented by an orange line. When the lines are equal to (-1), they parallel each other with the same slope. The dataset can’t even be correctly classified by this, so we need something extra that changes the slope of the line to classify it correctly.
We will be working on getting weights in place. Each feature of a Neuron must be accounted for in order to predict the output value. This function tells you whether or not there is a relationship between a particular feature in the dataset and the target value. An activation function that is shifted to the left of the right foot is referred to as bias activation. Consider a sigmoid activation function, which can be used to demonstrate bias in action. We could not change the center of the activation function if we gave different values of w, as it is in this case with the sigmoid function. Only by changing the value of bias(b) in the curve can it be shifted left or right.
The plot does not allow us to shift the curve in the opposite direction, but rather in the opposite direction. The curve equation is derived from the plot, and we can infer that all points to the left of x=5 appear to have y values less than 0.5, with rounded values resulting in a value of 0.1. It is this bias that allows the curve in an Artificial Neuron to shift to the right.
Neural Network Weights: How Important Are They?
A neural network’s weight is one of its most important features. The weight of each input is determined by how important it is in predicting the output. Neural networks are frequently used to make predictions based on data. Neural networks rely heavily on input data to generate predictions. Each input is given a value, or weight, that indicates how important it is in predicting the output, according to this definition. The weights are assigned to a neural network based on the random values that are used during initialized. After completing the training program, the weights should be adjusted so that the network is as accurate as possible. In most cases, the weight adjustment process entails comparing neural network predictions to those of a “test” neural network, which has been set to the same weights as the actual neural network but has not been trained. A neural network’s weights are usually denoted by a symbol, wij. In any parametric model, the parameters on the neural network are determined by their specific case. A neural network can calculate the weight of an input x by doing the following: *br When you add w(x) to it, you get w(x).
Weight Initialization Techniques
There are a few different weight initialization techniques that can be used in order to help train a neural network. One technique is to use random initialization, which involves randomly selecting values for the weights. Another technique is to use a zero initialization, which sets all of the weights to zero. There are also a few other techniques that can be used, such as using a pre-trained model or using a specific distribution for the weights.
Weights in neural networks are used to connect units, and while they can be initialized randomly and updated in the back propagation process, they are in charge of connection between units. The following are some of the techniques for initializing weight. The process of introducing new substances is referred to as normal or nave initialization. Normal distribution weights can be part of normal or gaussian distribution in terms of the mean-to-square and unit-to-standard deviation. As a result, it can be written as hyperparameter in Keras. According to Xavier and Glorot, if they maintain activation variance across all layers, backward convergence can be accelerated more quickly than using standard initialization where the gap is greater. It’s especially effective when used with tanh and sigmoid activations.
In contrast to tanh, ReLu has a standard deviation very close to the square root of 2 divided by its input connections. Tanh 1 should be used as a weight because it can be used as a base. Weights are distributed in a normal distribution where the mean is zero and the standard deviation is one. In Keras, it is simply as simple as adding a hyperparameter 2 to a Relu system as if some neural networks are deactivated or dead.
Why Weight Initialization Is Important
Weight initialization is needed for a variety of reasons. Furthermore, the method reduces the likelihood of layer activation outputs exploding or vanishing during a forward pass through deep neural networks. Furthermore, no initialization slows the optimization process by allowing the neuron to memorize the same functions repeatedly in multiple iterations. Choosing random initialization is a better option because initializing a large or small value can cause optimization to be slower.
Uniform Weight Initialization
One of the most important considerations when initializing the weights of a neural network is to ensure that the weights are set to a uniform value. This is because if the weights are set to a non-uniform value, the network will be unable to learn the correct mapping between the input and the output. There are many different ways to initialize the weights of a neural network, but uniform weight initialization is considered to be one of the most effective methods.
One of the most important factors in neural nets is the weight of the neuron. The three main weight initialization techniques will be discussed in this course. There are two options for uniform distribution: one at Xavier University and another at the University of Arizona. He’s still in the process of learning what he wants to know. Keras uses the Xavier(glorot) initializer for the majority of its operations. It is very easy to use the ReLU activation function with the weight initialization. ReLU activation, which is a non-linear method, is used in neural nets. When neurons’ weights are adjusted in such a way that the weighted sum of their inputs is zero, it is possible that half of them die. We can solve this problem by using variants of ReLU known as “Leaky ReLU,” “Parametric ReLU,” and “e.g., exponential linear units.”
The Importance Of Weight Initialization
If the network’s gradient does not have weight initialization, it may quickly grow to a large size, resulting in network instability. Deep neural networks trained on large amounts of data can be especially difficult to train on this basis. By initialization the weights, the gradient can be maintained throughout the network, preventing it from getting stuck or overfitting.

